
HMMs can, based on recorded data, shed light on unobservable (hidden) processes, categorized as states, such as the theoretical notion of disease status. Non-linear mixed effects models (NLMEs) are typically restrained to handle stochastic processes in observed variables in contrast, hidden Markov models (HMMs) are a class of statistical models that can be used to characterize relationships between observed variables and unobserved stochastic processes.
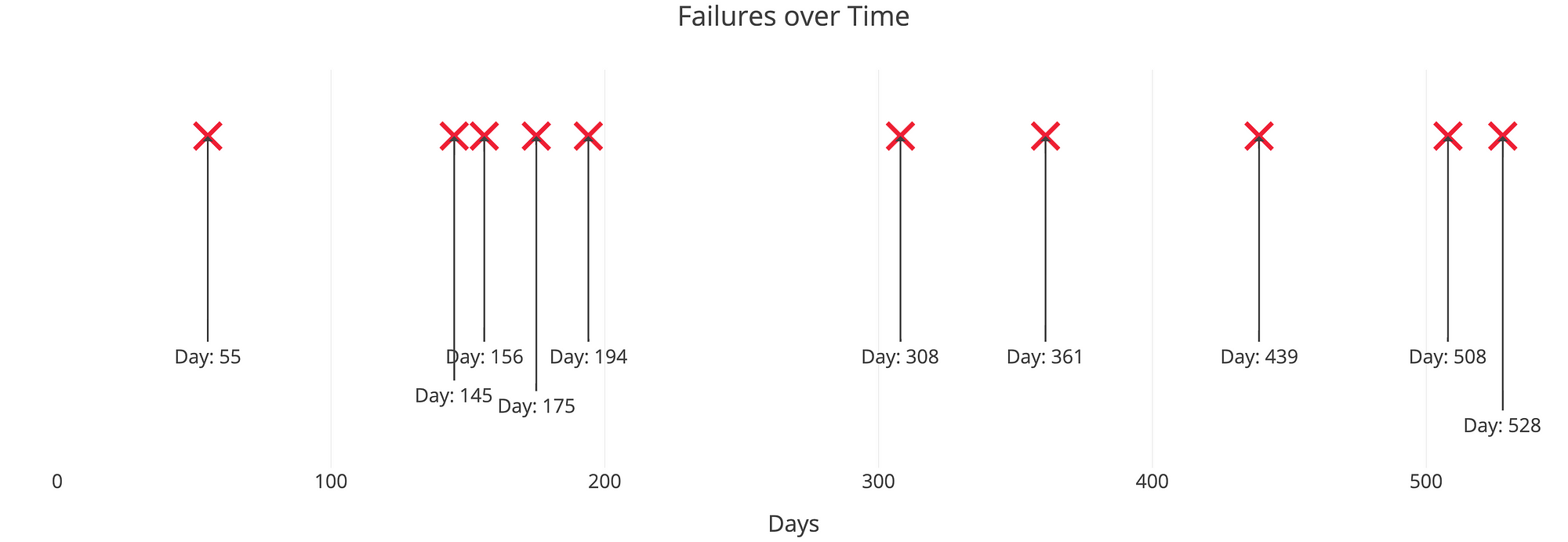
The results advocates for the use of bivariate MHMM models when implementation is possible. The power to detect the drug effect was improved by utilizing a bivariate MHMM model over the univariate MHMM models where the number of subject required for 80% power was 25 with the bivariate MHMM model versus 63 in the univariate MHMM FEV1 model and > 100 in the univariate MHMM PRO model. A drug effect was included on the transition rate probability and the precision of the drug effect parameter improved with increasing magnitude of the parameter. Parameter precision was better with higher magnitudes of the transition probability parameters. Parameter precision was high for all parameters with the exception of the variance of the transition rate dictating the transition from remission to exacerbation (relative root mean squared error > 150%). A bivariate MHMM was developed for simulating and analysing hypothetical COPD data consisting of PRO and FEV1 measurements collected every week for 60 weeks. The influence of including random and covariate effects of varying magnitudes on the parameters in the model was quantified and a power analysis was performed to compare the power of a single bivariate MHMM with two separate univariate MHMMs. Estimation properties in the software NONMEM of model parameters were investigated with and without random and covariate effect parameters. The two hidden states included in the model were remission and exacerbation and two observation sources were considered, patient reported outcomes (PROs) and forced expiratory volume (FEV1). In this work MHMMs were developed and applied in a chronic obstructive pulmonary disease example. Further, HMMs can be extended to include more than one observation source and are then multivariate HMMs.
Adding stochasticity to HMMs results in mixed HMMs (MHMMs) which potentially allow for the characterization of variability in unobservable processes. Hidden Markov models (HMMs) characterize the relationship between observed and hidden variables where the hidden variables can represent an underlying and unmeasurable disease status for example. Non-linear mixed effects models typically deal with stochasticity in observed processes but models accounting for only observed processes may not be the most appropriate for all data.


 0 kommentar(er)
0 kommentar(er)
